Linear Regression with One Variable

2019-08-02

2022-05-31

What is the linkear regression theory?

Regression theory is widely used in Computer Science nowadays. The main feature of this theory is this theory use the mathmatical function expression to predict future don’t know now. for that, the features of data should be expressed as a numeric one to make a mathematical function. and secondly we should find the best model represent the data.

if this model can be expressed as linear model. then it is usually named Linear Regression. let’s know about linear regression theory now.

3 steps of linear regression model.

Defining Hypothesis model.
Defining Cost function to calculate errors.
Minify the errors with Gradient Descent.

Defining Hypothesis model.

The hypothesis model is needed to generalize the data in regression theory. you should make a choice the hypothesis model before the calculation. if you choose the linear model for hypthesis than it would be called linear regression model.

Defining Cost function to calculate errors.

The errors means the difference between the real data and predicted data with hypothesis. if the errors is smaller than the hypothesis model is more fit with the data. if this model is good enough than you can extract valuable information with this hypothesis model.

Minify the errors with Gradient Descent.

we should find the way decrease errors enough to get optimized hypothesis model. Gradient Descent way is one of the solution can find the minimum of errors value point.

Hypothesis.

간단히 말해, 주어진 데이터들이 좌표평면 공간에 표현되어 있을 때 이를 가장 잘 표현할 수 있는 하나의 함수식, 모델을 결정하는 일이다. 이해를 위해 한가지 예를 들어 진행해보자. 아래의 그래프에 표현된 것은 ‘공부한 시간’과 ‘성적’의 관계에 대한 데이터다.

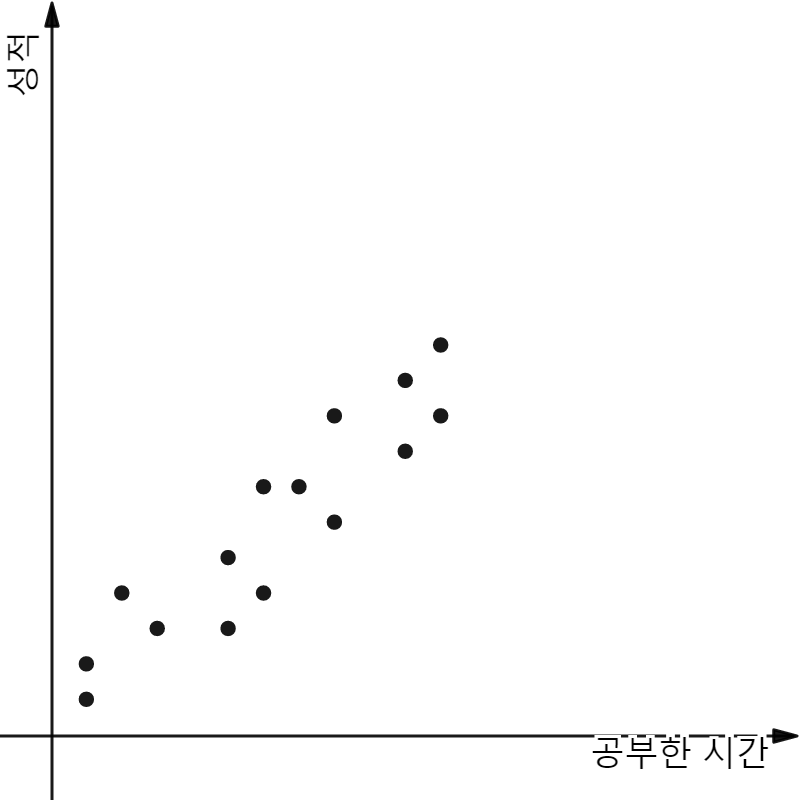
양의 상관관계를 가지는 ‘공부한 시간’, ‘성적’와 관련된 데이터들을 표현하기 위해 여러가지 모델들을 고려해 보자. 아래의 모델들이 충분히 후보군에 포함될 수 있을 것이다.

Candidate of Hypothesis Models

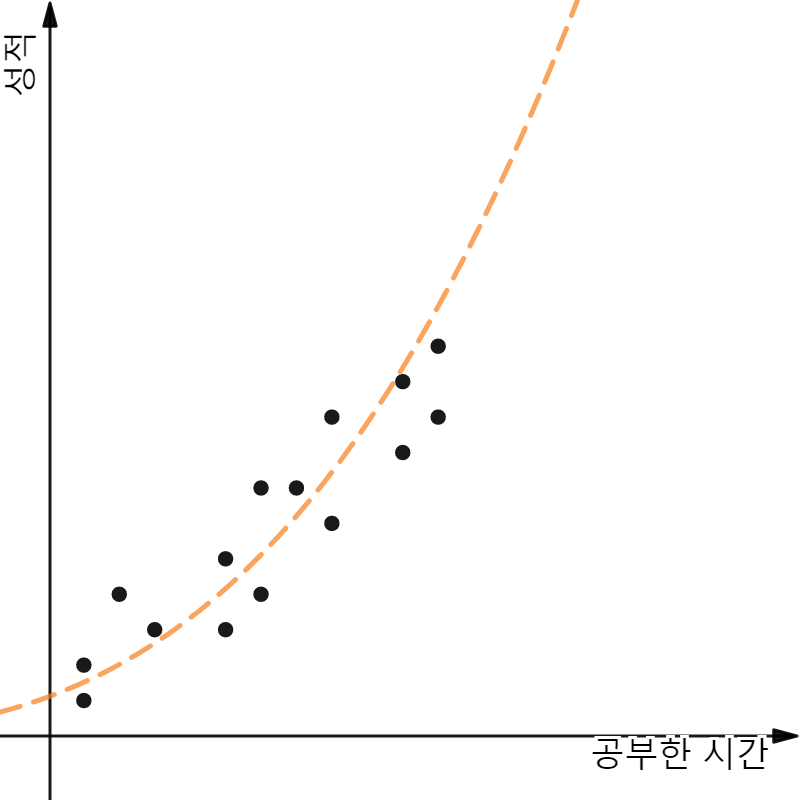
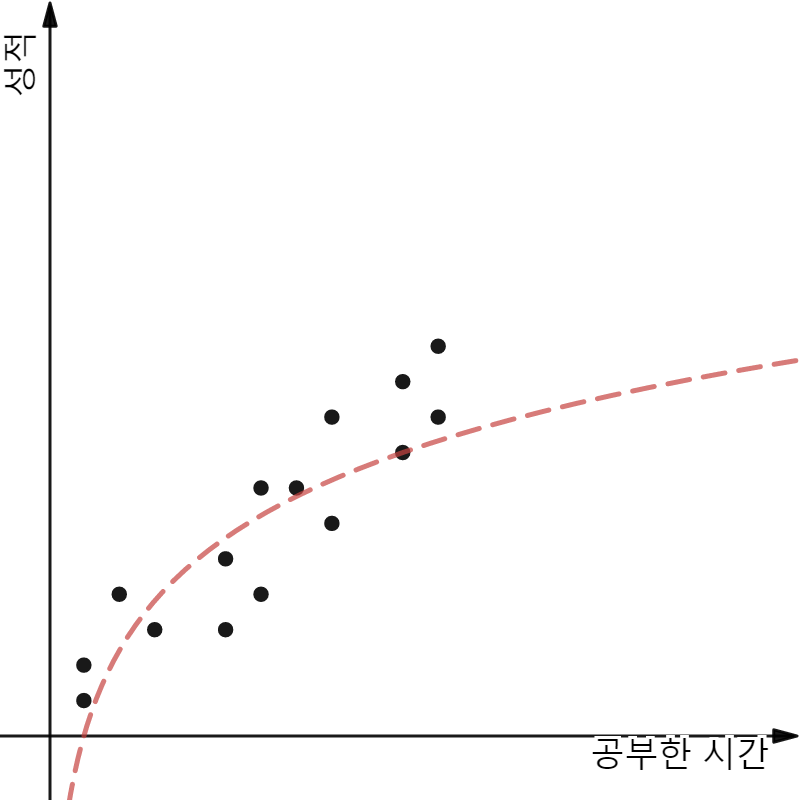
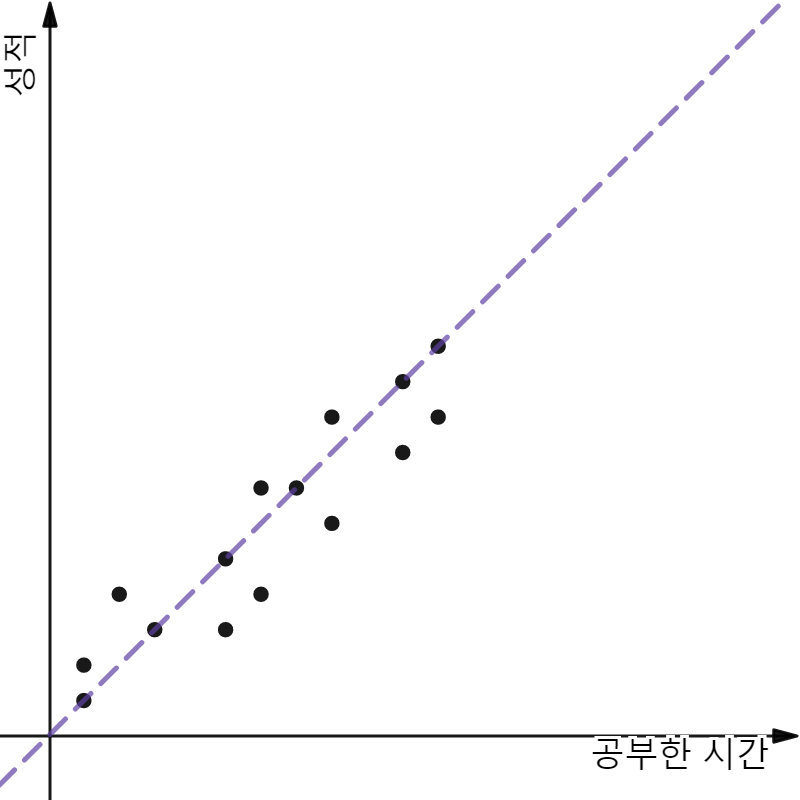
모두 보기에 합리적일 것 같은 후보 모델들이다. 여기서 나는 보라색 점선을 가진 3번째 모델을 선택하도록 하겠다. 그 이유는 모델이 일차함수로 만들어져 있기 때문이다.

실제로 이 데이터들을 표현하는 모델을 결정하는 일은 굉장히 중요하다. 모델을 보다 정확하게 하기 위해서는 보다 많은 데이터들을 가지는 것이 좋다. 또 좋은 모델을 결정하기 위한 일련의 절차가 있는데 이는 추후에 알아보도록 하자.

보라색 점선은 일차함수이다. 고로 분명 y = wx + b 함수식의 형태로 표현될 것이다. Linear Regression에서 궁극적으로 목표하는 것은 이 일차함수 식이 보라색 점선처럼 될 수 있도록 w, b 값을 유추해내는 것이다.

$model : y = wx + b$

그러나 이번 글에서는 보다 쉬운 이해를 이해 b 변수는 생략한 모델로 진행하도록 하겠다.

$Model : y = wx$

Cost Function. (에러의 정의와 산출)

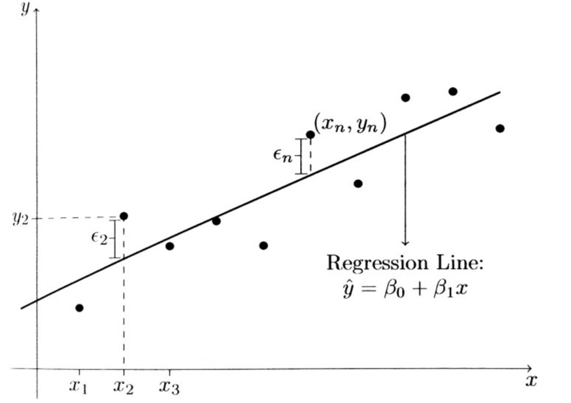
앞서 표현한 Hypothesis Model이 데이터를 가장 잘 표현하게 하기 위해서 Error의 개념을 사용하여 Cost Function을 정의한다.

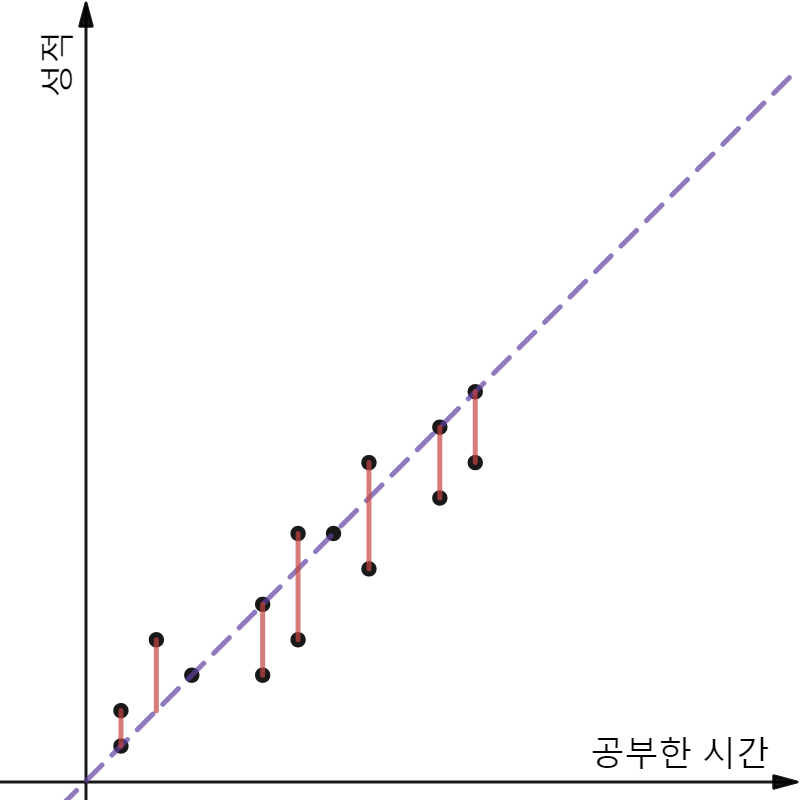
위 그래프를 보자. 검은 점들은 실제 데이터들을 나타내고 보라색 점선은 가설 모델이다. 그리고 빨간 실선은 실제 데이터와 모델을 통해 예측되어진 값의 차이를 보여준다. 이 값을 앞으로 Error라고 표현하겠다.

1	Error = 실제 데이터와 예측된 값의 차이

만약 위 그래프에 표현된 실제 데이터의 위치를 (x, y) 라고 한다면 Error는 다음과 같이 표현될 수 있다.

$Error = (wx - y)^2$

Error는 Scalar 값이기 때문에 부호를 없애기 위해서 제곱을 취했다. 자 이제 이 Error의 개념을 모든 데이터들에게 적용시켜 보자.

$Errors = \sum_{i=1}^{n} (wx_i - y_i)^2$

모든 데이터를 적용하기 위해 Error 수식에 i, n 변수를 사용했다. n은 데이터들의 총 개수를 뜻하며 i는 각 데이터들이다. 그러나 지금 이 수식은 완전하지 못하다. Error의 의미는 실제 데이터들과 모델을 통한 예측값의 차이를 표현하는 것인데 지금 수식을 통해서는 데이터가 많아져도 Error 값이 커진다. 이를 위해 n 값으로 나누어 주자.

$Errors = {1 \over n}\sum_{i=1}^{n} (wx_i - y_i)^2$

위와 같은 Error를 구하기 위한 방법론은 machine learning에만 국한된 것이 아닌 범용적으로 사용되는 알고리즘이다. 최소제곱법(Least Squared Method)라고 부르며 알고리즘 자체에 궁금한 것이 있다면 이를 검색해 찾아보자. 마지막으로 다음 단계인 Gradient Descent 에서는 미분을 진행한다. 이를 위해 계산을 편히 하기 위하여 미리 2로 나누어 주자.

$Cost Function = {1 \over 2n}\sum_{i=1}^{n} (wx_i - y_i)^2$

Gradient Descent (에러의 최소화)

Gradient Descent 단계를 진행하기 앞서 지금까지의 내용을 간략히 정리해 보자. Hypothesis 단계에서 데이터를 표현하기 위한 모델 하나를 결정 했다. 그리고 이 모델이 데이터를 가장 잘 표현하게 하기 위해서 Error의 개념을 도입했고 이 Error는 실제 데이터의 값과 모델을 통한 예측 값의 차이를 의미한다. 마지막으로 모든 데이터들의 Error 값을 합한 것이 Cost Function이였다. 즉 Cost Function은 실제 데이터 값과 예측 값의 차이의 합임으로 이 값이 최소화된다면 Model이 data를 잘 표현했다고 말할 수 있다.

$Model : y = wx$ $Cost Function = {1 \over 2n}\sum_{i=1}^{n} (wx_i - y_i)^2$

앞서 정의된 Cost Function을 최소화 시키기 위하여 경사감소법(Gradient Descent)를 활용한다. 이번엔 Cost Function의 그래프를 그려보도록 하자. 이 그래프는 이차함수로 표현된다. 이는 Cost Function의 수식을 살펴보거나 직접 값을 대입해보면 충분히 이해할 수 있을 것이다.

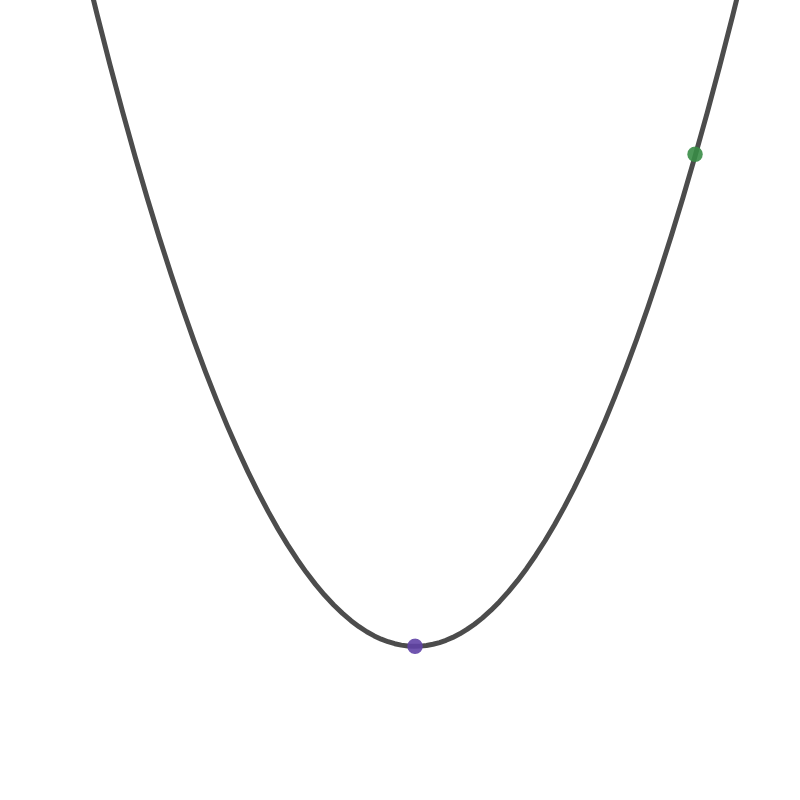
현재 Cost Function 그래프에 나타나 있는 초록색 점이 우리의 현재 값이라고 가정해보자. 이 값이 최소값을 가지게 하려면 보라색 점이 있는 곳 까지 도달해야 한다. 이를 위해 미분을 활용해보자. 미분은 그래프 상에서 접선의 기울기로 표현된다. 보라색 점에 도달하게 되면 그 때의 접선의 기울기는 0이기 때문에 미분 값을 0으로 볼 수 있다.

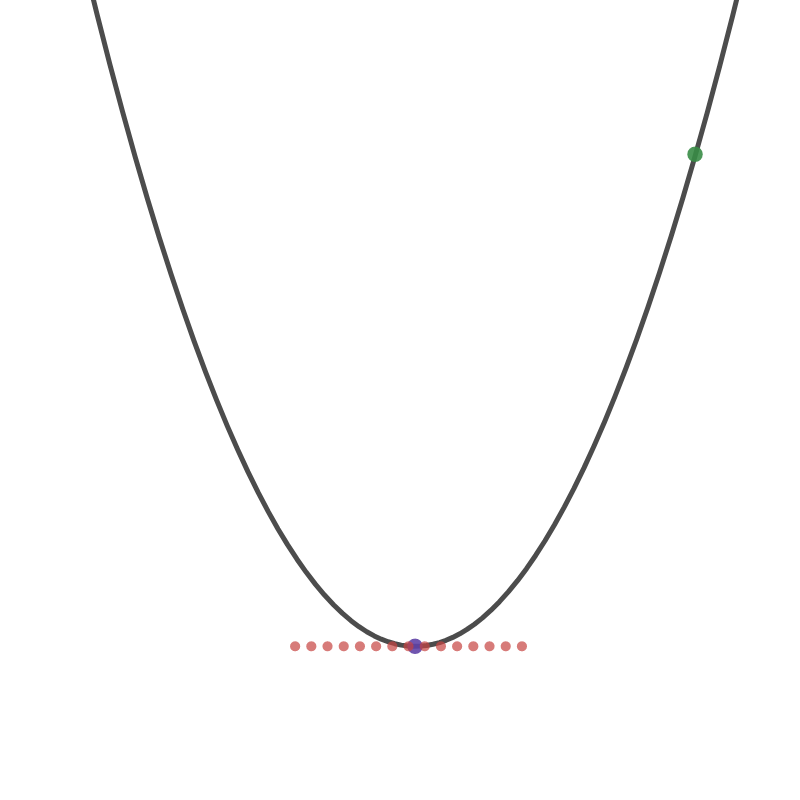
${ \partial \over \partial w } Cost Function = {1 \over n}\sum_{i=1}^{n} (wx_i - y_i) (x_i) = 0$

여기서 중요한 것은 현재 우리가 구하려는 것은 데이터를 가장 잘 표현하기 위한 모델임으로 결국 w의 값을 찾는 것임을 명심하자. 그렇기 때문에 w값 기준으로 미분하였다. x, y 값은 실제 데이터다.

앞에서 Cost Function의 미분 값이 0에 도달 했을 때 모델이 데이터를 가장 잘 표현한다는 것은 이해했다. 이제 0에 도달하기 위하여 Gradient Descent 방법을 활용한다. 이는 크게 어려운 것이 아니고 미분 값이 0에 도달할 때 까지 w값을 바꾸어 가며 반복하는 것이다.

$w_{n+1} = w_n - \alpha { \partial \over \partial w} Cost Function$

위의 수식이 Gradient Descent Cost Function의 미분 값이 0에 수렴하도록 계속 반복하면서 w의 값을 바꾸는 구조를 가지고 있다. alpha 값은 하이퍼 파라미터로 Gradient Descent의 반복할 때 값이 변하는 크기를 결정한다. 보통 learning rate라고 표현하며 자세히는 alpha : learning rate{: target=”_blank”} 글을 참고하라.

Summary

Machine Learning 분야에서 Linear Regression에 대해서 살펴보았다. 이는 Hypothesis, Cost Function, Gradient Descent 3단계로 구분되는데 Hypothesis에서 데이터들을 가장 잘 표현하기 위한 모델을 선정하였고 Linear Regression 이 모델이 일차함수로 나타난다. Cost Function을 통해 데이터과 모델의 차이를 정의하였고 이를 Gradient Descent 방법으로 최소화하여 데이터를 가장 잘 표현하는 모델을 만드는 방법을 알아보았다.

Tesorflow Example

import tensorflow as tf
import os

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'

x_train = [1.60, 1.63, 1.65, 1.66, 1.71, 1.70, 1.73, 1.70, 1.73]
y_train = [23.0, 23.5, 24.0, 23.5, 24.0, 24.0, 24.5, 24.0, 25.0]

a = tf.Variable(tf.random_normal([1]), name='a')
b = tf.Variable(tf.random_normal([1]), name='b')

hypothesis = a * x_train + b

e = tf.reduce_mean(tf.square(hypothesis - y_train))

optimizer =tf.train.GradientDescentOptimizer(learning_rate=0.01)
train = optimizer.minimize(e)

sess. tf.Session()
sess.run(tf.global_variables_initializer())

for step in range(2001) :
    sess.run(train)

    if step % 20 == 0 :
        print("Iteration : ", step, " e : ", sess.run(e), " ( y =", sess.run(a), " x + ", sess.run(b), ")" )

Devlog