Devlog

Linear Regression with Weight, Bias

선형 회귀 이론의 확장.

기존의 선형회귀 이론은 Hypothesis 모델이 y = wx 로 구하려고 하는 변수가 w값 1개 였다.
그러나 실제로 이렇게 단순한 모델로 적용할 수 있는 상황은 그렇게 많지 않다. 이번에는 생략했던 b값도 추가하여 y = wx + b 의 모델로 선형 회귀 이론에 대해서 알아보자.

Hypothesis

개념은 Linear Regression with One Variable 와 동일하다. 다만 모델이 y = wx + b 로 생략되었던 b를 추가하여 진행한다. 궁극적으로 이 모델이 데이터를 잘 표현하기 위한 w, b 두개의 값을 구해야 한다.


Cost Function

마찬가지로 개념은 동일하지만 Hypothesis 모델이 변함으로 인해 수식이 조금은 변경된다. 아래를 확인하자.

이제 Cost Function을 그래프로 그리기 위해서는 좌표평면으로는 부족하다. 잘 생각해보면 Error를 w, b 2가지의 관점에서 고려해야 하기 떄문이다. 즉 고려해야할 변수가 1개가 아닌 2개로 늘어났다. 아마 이를 시각화 시키면 아래와 같다.

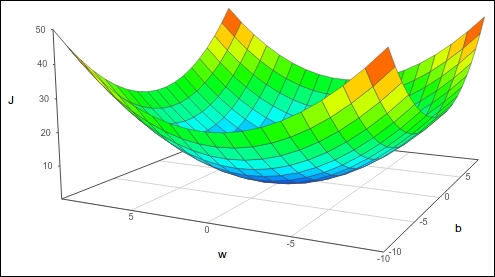
그래프에서 y축에 해당하는 J는 Error와 동일하며 x, z 축이 w와 b값을 의미하고 있다. Cost가 최소값을 가지도록 w, b 값을 조절해야한다. Gradient Descent 방법을 활용하여 해결하자.

Contour Plot

그래프를 3차원으로 표현하는 것은 사람에게 익숙하지 않다. 따라서 위와 같은 Cost Function을 2차원으로 표현하기 위해 Contour Plot 그래프를 자주 사용한다.

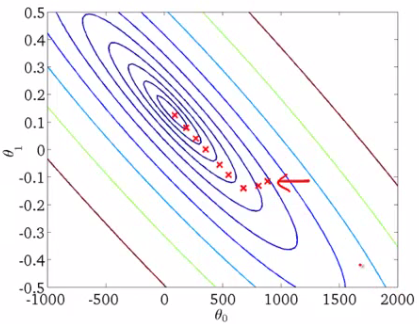
이 그래프는 y축 즉 하늘에서 아래로 바라보는 방향을 가지고 있으며 색상을 통해서 Error 값이 높은지 낮은지를 표현한다. 가운데로 갈수록 진한 파란색으로 표현되는데 이는 에러가 낮음을, 붉은색은 높음을 표현하고 있다. 빨간 x표시는 현재 모델의 에러 값을 나타내는 것이며 Gradient Descent 학습을 통해 점점 최소값으로 다가가고 있음을 나타낸다.

Gradient Descent

적용하는 방법은 변수 1개일 때와 다른 것이 없다. 다만 변수가 2개임으로 편미분을 진행해야 한다. 즉 하나는 w를 기준으로, 다른 하나는 b를 기준으로 미분해야한다.

Partial Derivative based w.

Partial Derivative based b.

중요한것은 각 반복마다 이 편미분된 값들이 업데이트 될때 서로가 영향을 미치지 않으며 동시에 업데이트가 되어야 한다. 즉 코드를 작성할 때 어떤 연산의 우선순위를 갖고 다른 값에 변화를 주면 안된다.

최종적인 Gradient Descent 알고리즘이다. 지속적인 반복을 통해 w와 b값을 최소값에 다다르게 하면 Hypothesis Model은 데이터를 잘 표현할 수 있다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import tensorflow as tf
import os

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'

x_train = [1.60, 1.63, 1.65, 1.66, 1.71, 1.70, 1.73, 1.70, 1.73]
y_train = [23.0, 23.5, 24.0, 23.5, 24.0, 24.0, 24.5, 24.0, 25.0]

a = tf.Variable(tf.random_normal([1]), name='a')
b = tf.Variable(tf.random_normal([1]), name='b')

hypothesis = a * x_train + b

e = tf.reduce_mean(tf.square(hypothesis - y_train))

optimizer =tf.train.GradientDescentOptimizer(learning_rate=0.01)
train = optimizer.minimize(e)

sess. tf.Session()
sess.run(tf.global_variables_initializer())

for step in range(2001) :
    sess.run(train)

    if step % 20 == 0 :
        print("Iteration : ", step, " e : ", sess.run(e), " ( y =", sess.run(a), " x + ", sess.run(b), ")" )
Share